Robohub.org
DART: Noise injection for robust imitation learning

Toyota HSR Trained with DART to Make a Bed.
By Michael Laskey, Jonathan Lee, and Ken Goldberg
In Imitation Learning (IL), also known as Learning from Demonstration (LfD), a robot learns a control policy from analyzing demonstrations of the policy performed by an algorithmic or human supervisor. For example, to teach a robot make a bed, a human would tele-operate a robot to perform the task to provide examples. The robot then learns a control policy, mapping from images/states to actions which we hope will generalize to states that were not encountered during training.
There are two variants of IL: Off-Policy, or Behavior Cloning, where the demonstrations are given independent of the robot’s policy. However, when the robot encounters novel risky states it may not have learned corrective actions. This occurs because of “covariate shift” a known challenge, where the states encountered during training differ from the states encountered during testing, reducing robustness. Common approaches to reduce covariate shift are On-Policy methods, such as DAgger, where the evolving robot’s policy is executed and the supervisor provides corrective feedback. However, On-Policy methods can be difficult for human supervisors, potentially dangerous, and computationally expensive.
This post presents a robust Off-Policy algorithm called DART and summarizes how injecting noise into the supervisor’s actions can improve robustness. The injected noise allows the supervisor to provide corrective examples for the type of errors the trained robot is likely to make. However, because the optimized noise is small, it alleviates the difficulties of On-Policy methods. Details on DART are in a paper that will be presented at the 1st Conference on Robot Learning in November.
We evaluate DART in simulation with an algorithmic supervisor on MuJoCo tasks (Walker, Humanoid, Hopper, Half-Cheetah) and physical experiments with human supervisors training a Toyota HSR robot to perform grasping in clutter, where a robot must search through clutter for a goal object. Finally, we show how DART can be applied in a complex system that leverages both classical robotics and learning techniques to teach the first robot to make a bed. For researchers who want to study and use robust Off-Policy approaches, we additionally announce the release of our codebase on GitHub.
Imitation Learning’s Compounding Errors
In the late 80s, Behavior Cloning was applied to teach cars how to drive, with a project known as ALVINN (Autonomous Land Vehicle in a Neural Network). In ALVINN, a neural network was trained on driving demonstrations and learned a policy that mapped images of the road to the supervisor’s steering angle. Unfortunately, after learning, the policy was unstable, as indicated in the following video:

ALVINN Suffering from Covariate Shift.
The car would start drifting to side of the road and not know how to recover. The reason for the car’s instability was that no data was collected on the side of the road. During the data collection the supervisor always drove along the center of the road; however, if the robot began to drift from the demonstrations, it would not know how to recover because it saw no examples.
This example, along with many others that researchers have tried, shows that Imitation Learning cannot be entirely solved with Behavior Cloning. In traditional Supervised Learning, the training distribution is de-coupled from the learned model, whereas in Imitation Learning, the robot’s policy affects what state is queried next. Thus the training and testing distributions are no longer equivalent, and this mismatch is known as covariate shift.
To reduce covariate shift, the objective of Imitation Learning had to be modified. The robot should now be expected to match the supervisor on the states it is likely to visit. Thus, if ALVINN is likely to drift to the side of the road, we expect that it will know what to do in those states.
A robot’s policy and a supervisor’s policy can be denoted as $\pi_{\theta}$ and , where $\pi$ is a function mapping state to action and $\theta$ is a parametrization, like weights in a neural network. We can measure how close two policies are by what actions they apply at a given state, which we refer to as the surrogate loss, $l$. A common surrogate loss is the squared Euclidean distance:
Finally, we need a distribution over trajectories $p(\xi|\theta)$, which indicate the trajectories, $\xi$, that are likely under the current policy $\pi_{\theta}$. Our objective can then be written as follows:
Hence we want to minimize the expected surrogate loss on the distribution of states induced by the robot’s policy. This objective is challenging to solve because we don’t know what the robot’s policy is until after data has been collected, which creates a chicken and egg situation. We will now discuss an iterative On-Policy approach to overcome this problem.
Reducing Shift with On-Policy Methods
A large body of work from Ross and Bagnell [6,7], has examined the theoretical consequences of covariate shift. In particular, they proposed the DAgger algorithm to help correct for it. DAgger can be thought of as an On-Policy algorithm — which rolls out the current robot policy during learning.
The key idea of DAgger is to collect data from the current robot policy and update the model on the aggregate dataset. Implementation of DAgger requires iteratively rolling out the current robot policy, querying a supervisor for feedback on the states visited by the robot, and then updating the robot on the aggregate dataset across all iterations.

The DAgger Algorithm.
Two years ago, we used DAgger to teach a robot to perform grasping in clutter (shown below), which requires a robot to search through objects via pushing to reach a desired goal object. Imitation Learning was advantageous in this task because we didn’t need to explicitly model the collision of multiple non-convex objects.

Planar Grasping in Clutter.
Our planar robot had a neural network policy that mapped images of the workspace to a control signal. We trained it with DAgger on 160 expert demonstrations. While we were able to teach the robot how to perform the task with a 90% success rate, we encountered several major hurdles that made it challenging to increase the complexity of the task.
Challenges with On-Policy Methods
After applying DAgger to teach our robot, we wanted to study and better understand 3 key limitations related to On-Policy methods in order to scale up to more challenging tasks.
Limitation 1: Providing Feedback
In order to apply feedback to our robot, we had to do so retroactively with a labeling interface, shown below.

Supervisor Providing Retroactive Feedback.
A supervisor had to manually move the pink overlay to tell the robot what it should have done after execution. When we tried to retrain the robot with different supervisors, we found it was very challenging to provide this feedback for most people. You can think of a human supervisor as a controller that needs to constantly adjust their actions to obtain the desired effect. However, with retroactive feedback the human must simulate what the action would be without seeing the outcome, which is quite unnatural.
To test this hypothesis, we performed a human study with 10 participants to compare DAgger against Behavior Cloning, where each participant was asked to train a robot to perform planar part singulation. We found that Behavior Cloning out-performed DAgger, suggesting that while DAgger mitigates the shift, in practice it may add systematic noise to the supervisor’s signal [2].
Limitation 2: Safety
On-Policy methods have the additional burden of needing to roll-out the current robot’s policy during execution. While our robot was able to perform the task at the end of training, for most of learning it wasn’t successful:

Robot Rolling Out Unsuccessful Policy.
In unstructured environments, such as a self-driving car or home robotics, this can be problematic. Ideally, we would like to collect data with the robot while maintaining high performance throughout the entire process.
Limitation 3: Computation
Finally, when building systems either in simulation or the real world, we want to collect large amounts of data in parallel and update our policy sparingly. Neural networks can require significant computation time for retraining. However, On-Policy methods suffer when the policy is not updated frequently during data collection. Training on a large batch size of new data can cause significant changes to the current policy, which can push the robot’s distribution away from the previously collected data and make the aggregate dataset stale.
Variants of On-Policy methods have been proposed to solve each of these problems individually. For example, Ho et al. got rid of the retroactive feedback by proposing, GAIL, which uses Reinforcement Learning to reduce covariate shift [8]. Zhang et al. examined how to detect when the policy is about to deviate to a risky state and asks the supervisor to take over [4]. Sun et al. has explored incremental gradient updates to the model instead of a full retrain, which is computationally cheaper [5].
While these methods can each solve some of these problems, ideally we want a solution to address all three. Off-Policy algorithms like Behavior Cloning do not exhibit these problems because they passively sample from the supervisor’s policy. Thus, we decided instead of extending On-Policy methods it might be more beneficial to make Off-Policy methods more robust.
Off-Policy with Noise Injection
Off-Policy methods, like Behavior Cloning, can in fact have low covariate shift. If the robot is able to learn the supervisor’s policy perfectly, then it should visit the same states as the supervisor. In prior work we empirically found in simulation that with sufficient data and expressive learners, such as deep neural networks, Behavior Cloning is at parity with DAgger [2].
In real world domains, though, it is unlikely that a robot can perfectly match a supervisor. Machine Learning algorithms generally have a long tail in terms of sample complexity, so the amount of data and computation needed to perfectly match a supervisor may be unreasonable. However, it is likely that we can achieve small non-zero test error.
Instead of attempting to perfectly learn the supervisor, we propose simulating small amounts of error in the supervisor’s policy to better mimic the trained robot. Injecting noise into the supervisor’s policy during teleoperation is one way to simulate this small test error during data collection. Noise injection forces the supervisor to provide corrective examples to these small disturbances as they try to perform the task. Shown below is the intuition of how noise injection creates a funnel of corrective examples around the supervisor’s distribution.
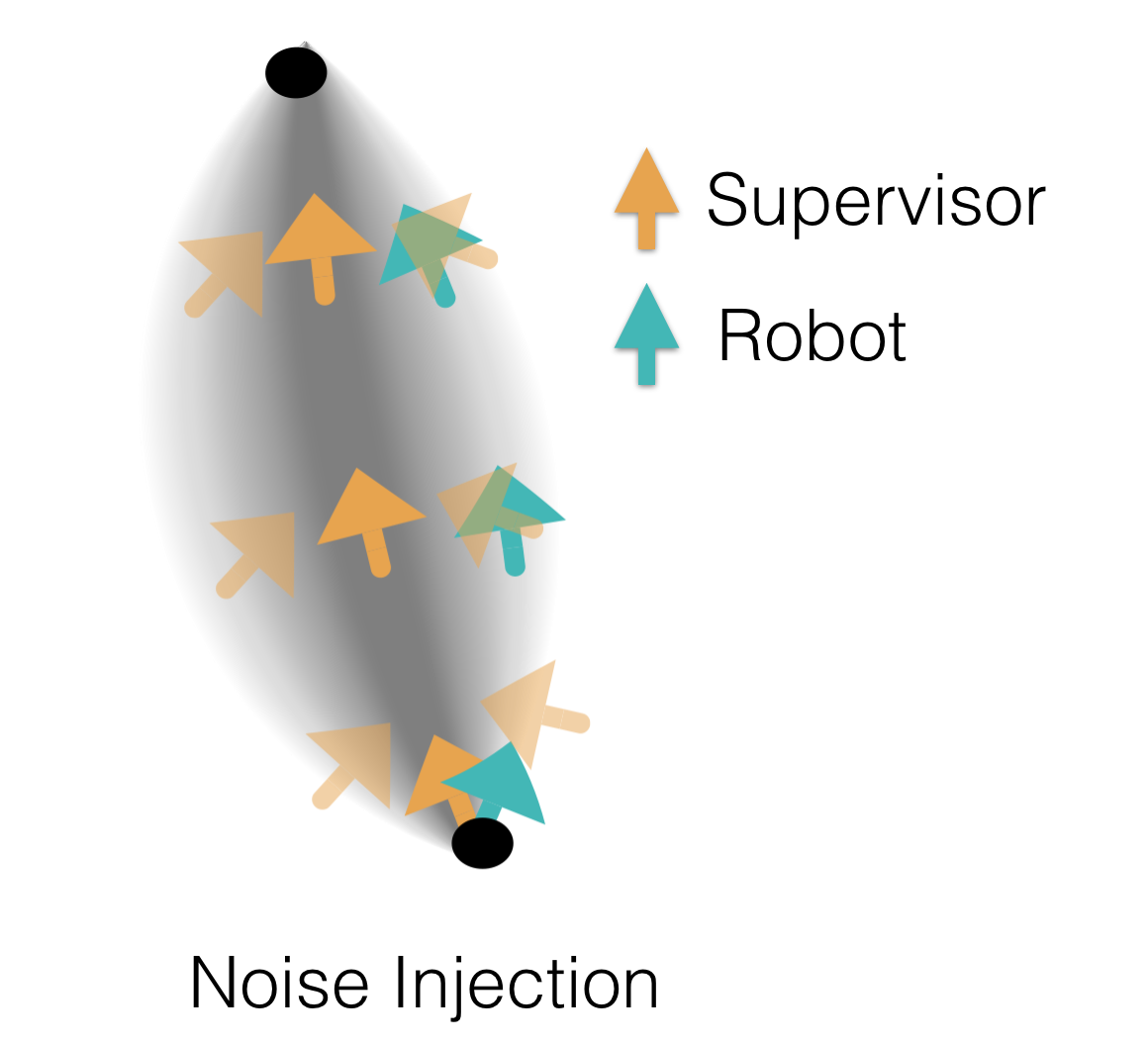
Noise Injection forces the supervisor to provide corrective examples,
so that the robot can learn to recover.
Additionally, because we are only injecting small noise levels, we don’t suffer as many limitations compared to On-Policy methods. A supervisor can normally be robust to small random disturbances that are concentrated around their current action. We will now formalize noise injection a bit to help understand its effect more.
Denote by a distribution over trajectories with noise injected into the supervisor’s distribution . The parameter $\psi$ represents the sufficient statistics that define the noise distribution. For example, if Gaussian noise is injected parameterized by $\psi$, then . Note, the stochastic supervisor’s distribution is a slight abuse of notation. is a distribution over actions, where as is a deterministic function mapping to a single action.
Similar to Behavior Cloning, we can sample demonstrations from the noise-injected supervisor and minimize the expected loss via standard supervised learning techniques:
This equation, though, does not explicitly minimize the covariate shift for arbitrary choices of $\psi$; the $\psi$ needs to be chosen to best simulate the error of the final robot’s policy, which may be complex for high dimensional action spaces. One approach to choose $\psi$ is grid-search, but this requires expensive data collection, which can be prohibitive in the physical world or in high fidelity simulation.
Instead of grid-search, we can formulate the selection of $\psi$ as a maximum likelihood problem. The objective is to increase the probability of the supervisor applying the robot’s control.
This objective states that we want the noise injected supervisor to try and match the final robot’s policy. In the paper, we show that this explicitly minimizes the distance between the supervisor and robot’s distribution. A clear limitation of this optimization problem though is that it requires knowing the final robot’s distribution $p(\xi|\pi_{\theta^R})$, which is determined only after the data is collected. In the next section, we present DART, which applies an iterative approach to the optimization.
DART: Disturbances for Augmenting Robot Trajectories
The above objective cannot be solved because $p(\xi|\pi_{\theta^R})$ is not known until after the robot has been trained. We can instead iteratively sample from the supervisor’s distribution with the current noise parameter, $\psi_k$, and minimize the negative log-likelihood of the noise-injected supervisor taking the current robot’s, $\pi_{\hat{\theta}}$, control.
The above iterative process can be slow to converge because it is optimizing the noise with respect to the current robot’s policy. We can obtain a better estimate by observing that the supervisor should simulate as much expected error as the final robot policy, . It is possible that we have some knowledge of this quantity from previously training on similar domains. In the paper, we show how to incorporate this knowledge in the form of a prior. For some common noise distributions, the objective can be solved in closed form, as detailed in the paper. Thus, the optimization problem determines the shape of the noise injected and the prior helps determine the magnitude.
Our algorithm DART, iteratively solves this optimization problem to best set the noise term. DART is still an iterative algorithm like On-Policy methods. Through the iterative process, DART optimizes $\psi$ to better simulate the error in the final robot’s policy.
Evaluating DART
To understand how effectively DART reduces covariate shift and to determine if it suffers from similar limitations as On-Policy methods, we ran experiments in 4 MuJoco domains, as shown below. The supervisor was a policy trained with TRPO and the noise we injected was Gaussian.

To test if DART suffers from updating the policy after larger batches, we only updated the model after every $K$ demonstrations for all experiments. DAgger was updated after every demonstration and DAgger-B was updated after every $K$. The results show that DART is able to have the same performance as DAgger, but is significantly faster in terms of computation. DAgger-B is relatively similar in computation time, but suffers significantly in performance, suggesting DART can significantly reduce computation time.
We finally compared DART to Behavior Cloning in a human study for the task of grasping in clutter, shown below. In the task, a Toyota HSR robot was trained to reach a goal object by pushing objects away with its gripper.

Toyota HSR Trained with DART for Grasping in Clutter.
The task is more complex than the one above because the robot now sees images of the world taken from an eye-in-hand camera. We compared 4 humans subjects and saw that by injecting noise in the controller, we were able to receive a win over Behavior Cloning of 62%. DART was able to reduce the shift on the task with human supervisors.
Robotic Bed Making: A Testbed for Covariate Shift
To better understand how errors compound in real world robotic systems, we built a literal test bed. Robotic Bed Making has been a challenging task in robotics due to it requiring mobile manipulation of deformable objects and sequential planning. Imitation Learning is one way to sidestep some of the challenges of deformable object manipulation because it doesn’t require modeling the bed sheets.
The goal of our bed making system was to have a robot learn to stretch the sheets over the bed frame. The task was designed so that the robot must learn one policy to decide where to grasp the bed sheet and another transition policy to decide whether the robot should try again or switch to the other bed side. We trained the bed making policy with 50 demonstrations.

Bed Making System.
DART was applied to inject Gaussian noise into grasping policy because we assumed there would be considerable error in determining where to grasp. The optimized covariance matrix decided to inject more noise in the horizontal direction of the bed, because that is where the edge of the sheet varied more significantly and subsequently the robot had higher error.
In order to test how large covariate shift was in the system, we can take our trained policy $\pi_{\theta^R}$ and write its performance with the following decomposition.
where the first term on the right-hand side corresponds to the covariate shift. Intuitively, the covariate shift is the difference between the expected error on the robot’s distribution and the supervisor’s distribution. When we measured these quantities on the bed making setup, we observed noticeable covariate shift in the transition policy trained with Behavior Cloning.

Covariate Shift in Bed Making Task.
We attribute this covariate shift due to the fact that with Behavior Cloning the robot rarely saw unsuccessful demonstrations; thus the transition policy never knew what failure was. DART gave a more diverse set of states, which allowed the policy to have better class balance. DART was able to train a robust policy that allowed it to perform the bed making task even when novel objects were placed on the bed, as shown at the beginning of the blog post. When distractor objects are placed on the bed DART obtained a 97% sheet coverage, whereas Behavior Cloning achieved only 63%.
These initial results suggest that covariate shift can occur in modern day systems that use learning components. We will soon release a longer preprint on the Bed Making Setup for more information.
DART presents a way to correct for shift via the injection of small optimized noise. Going forward, we are considering more complex noise models that better capture the temporal structure of the robot’s error.
(For papers and updated information, see UC Berkeley’s AUTOLAB website.)
This article was initially published on the BAIR blog, and appears here with the authors’ permission.
References
-
Michael Laskey, Jonathan Lee, Roy Fox, Anca Dragan, Ken Goldberg ; DART: Noise Injection for Robust Imitation Learning Proceedings of the 1st Annual Conference on Robot Learning, PMLR 78:143-156, 2017.
-
M. Laskey, C. Chuck, J. Lee, J. Mahler, S. Krishnan, K. Jamieson, A. Dragan, and K. Goldberg. Comparing human-centric and robot-centric sampling for robot deep learning from demonstrations. Robotics and Automation (ICRA), 2017 IEEE International Conference on, pages 358-365. IEEE, 2017
-
M. Laskey, J. Lee, C. Chuck, D. Gealy, W. Hsieh, F. T. Pokorny, A. D. Dragan, and K. Goldberg. Robot grasping in clutter: Using a hierarchy of supervisors for learning from demonstrations. In Automation Science and Engineering (CASE), 2016 IEEE International Conference on, pages 827–834. IEEE, 2016.
-
Zhang, Jiakai, and Kyunghyun Cho. “Query-Efficient Imitation Learning for End-to-End Simulated Driving.” In AAAI, pp. 2891-2897. 2017.
-
W. Sun, A. Venkatraman, G. J. Gordon, B. Boots, and J. A. Bagnell. Deeply aggrevated: Differentiable imitation learning for sequential prediction. Proceedings of the 34th International Conference on Machine Learning, PMLR 70:3309-3318, 2017.
-
Ross, Stéphane, Geoffrey J. Gordon, and Drew Bagnell. “A reduction of imitation learning and structured prediction to no-regret online learning.” International Conference on Artificial Intelligence and Statistics. 2011.
-
S. Ross and D. Bagnell. Efficient reductions for imitation learning. In International Conference on Artificial Intelligence and Statistics, pages 661–668, 2010.
-
Ho, Jonathan, and Stefano Ermon. “Generative adversarial imitation learning.” Advances in Neural Information Processing Systems. 2016.