Robohub.org
When recurrent models don’t need to be recurrent
By John Miller
An earlier version of this post was published on Off the Convex Path. It is reposted here with the author’s permission.
In the last few years, deep learning practitioners have proposed a litany of different sequence models. Although recurrent neural networks were once the tool of choice, now models like the autoregressive Wavenet or the Transformer are replacing RNNs on a diverse set of tasks. In this post, we explore the trade-offs between recurrent and feed-forward models.
Feed-forward models can offer improvements in training stability and speed, while recurrent models are strictly more expressive. Intriguingly, this added expressivity does not seem to boost the performance of recurrent models. Several groups have shown feed-forward networks can match the results of the best recurrent models on benchmark sequence tasks. This phenomenon raises an interesting question for theoretical investigation:
When and why can feed-forward networks replace recurrent neural networks without a loss in performance?
We discuss several proposed answers to this question and highlight our recent work that offers an explanation in terms of a fundamental stability property.
A Tale of Two Sequence Models
Recurrent Neural Networks
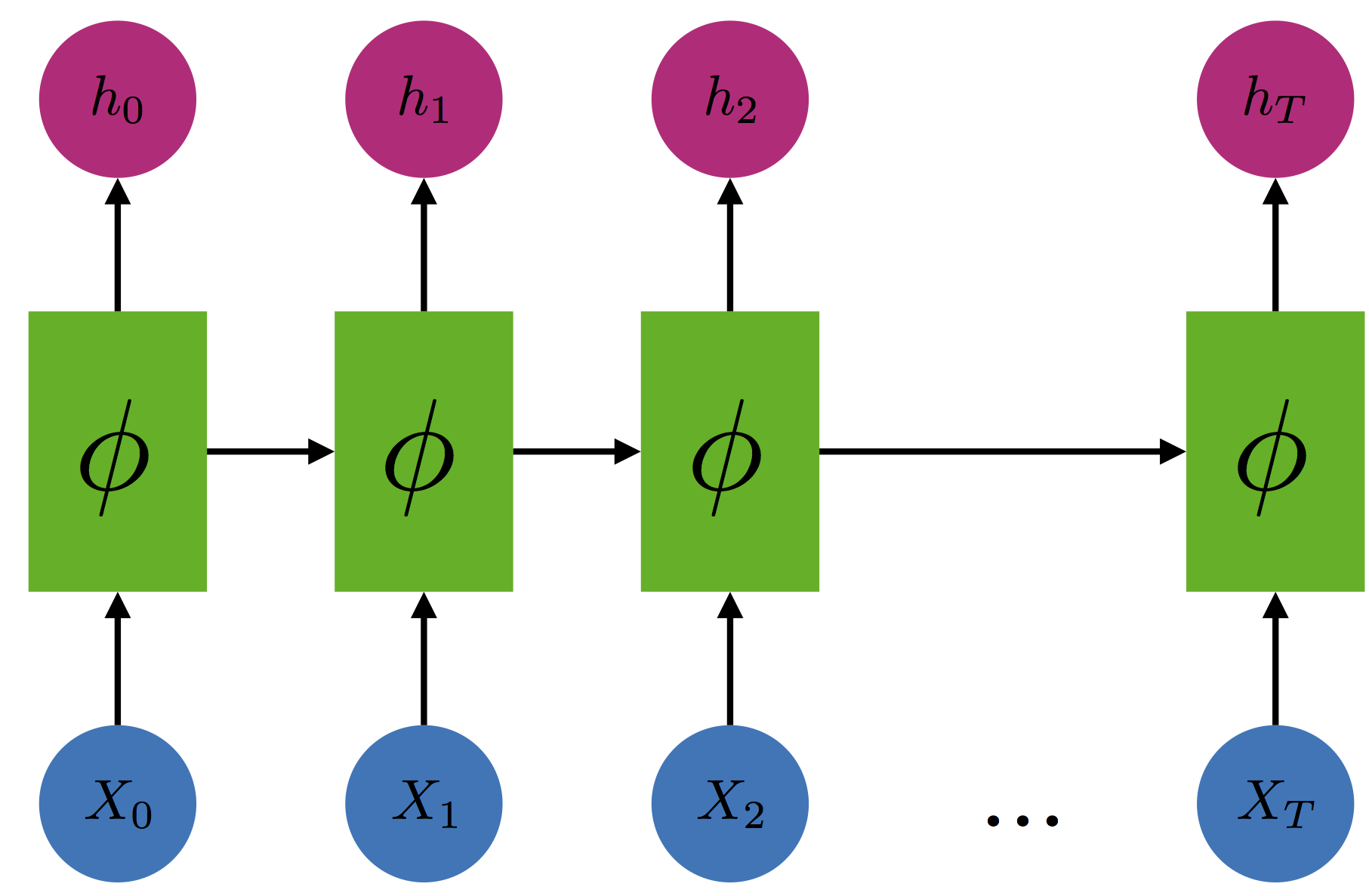
The many variants of recurrent models all have a similar form. The model maintains a state $h_t$ that summarizes the past sequence of inputs. At each time step $t$, the state is updated according to the equation
where $x_t$ is the input at time $t$, $\phi$ is a differentiable map, and $h_0$ is an initial state. In a vanilla recurrent neural network, the model is parameterized by matrices $W$ and $U$, and the state is updated according to
In practice, the Long Short-Term Memory (LSTM) network is more frequently used. In either case, to make predictions, the state is passed to a function $f$, and the model predicts $y_t = f(h_t)$. Since the state $h_t$ is a function of all of the past inputs $x_0, \dots, x_t$, the prediction $y_t$ depends on the entire history $x_0, \dots, x_t$ as well.
A recurrent model can also be represented graphically.
Recurrent models are fit to data using backpropagation. However, backpropagating gradients from time step $T$ to time step $0$ often requires infeasibly large amounts of memory, so essentially every implementation of a recurrent model truncates the model and only backpropagates gradient $k$ times steps.

In this setup, the predictions of the recurrent model still depend on the entire history $x_0, \dots, x_T$. However, it’s not clear how this training procedure affects the model’s ability to learn long-term patterns, particularly those that require more than $k$ steps.
Autoregressive, Feed-Forward Models
Instead of making predictions from a state that depends on the entire history, an autoregressive model directly predicts $y_t$ using only the $k$ most recent inputs, $x_{t-k+1}, \dots, x_{t}$. This corresponds to a strong conditional independence assumption. In particular, a feed-forward model assumes the target only depends on the $k$ most recent inputs. Google’s WaveNet nicely illustrates this general principle.

In contrast to an RNN, the limited context of a feed-forward model means that it cannot capture patterns that extend more than $k$ steps. However, using techniques like dilated-convolutions, one can make $k$ quite large.
Why Care About Feed-Forward Models?
At the outset, recurrent models appear to be a strictly more flexible and expressive model class than feed-forward models. After all, feed-forward networks make a strong conditional independence assumption that recurrent models don’t make. Even if feed-forward models are less expressive, there are still several reasons one might prefer a feed-forward network.
- Parallelization: Convolutional feed-forward models are easier to parallelize at training time. There’s no hidden state to update and maintain, and therefore no sequential dependencies between outputs. This allows very efficient implementations of training on modern hardware.
- Trainability: Training deep convolutional neural networks is the bread-and-butter of deep learning. Whereas recurrent models are often more finicky and difficult to optimize, significant effort has gone into designing architectures and software to efficiently and reliably train deep feed-forward networks.
- Inference Speed: In some cases, feed-forward models can be significantly more light-weight and perform inference faster than similar recurrent systems. In other cases, particularly for long sequences, autoregressive inference is a large bottleneck and requires significant engineering work or significant cleverness to overcome.
Feed-Forward Models Can Outperform Recurrent Models
Although it appears trainability and parallelization for feed-forward models comes at the price of reduced accuracy, there have been several recent examples showing that feed-forward networks can actually achieve the same accuracies as their recurrent counterparts on benchmark tasks.
-
Language Modeling. In language modeling, the goal is to predict the next word in a document given all of the previous words. Feed-forward models make predictions using only the $k$ most recent words, whereas recurrent models can potentially use the entire document. The Gated-Convolutional Language Model is a feed-forward autoregressive models that is competitive with large LSTM baseline models. Despite using a truncation length of $k=25$, the model outperforms a large LSTM on the Wikitext-103 benchmark, which is designed to reward models that capture long-term dependencies. On the Billion Word Benchmark, the model is slightly worse than the largest LSTM, but is faster to train and uses fewer resources.
-
Machine Translation. The goal in machine translation is to map sequences of English words to sequences of, say, French words. Feed-forward models make translations using only $k$ words of the sentence, whereas recurrent models can leverage the entire sentence. Within the deep learning world, variants of the LSTM-based Sequence to Sequence with Attention model, particularly Google Neural Machine Translation, were superseded first by a fully convolutional sequence to sequence model and then by the Transformer.1

-
Speech Synthesis. In speech synthesis, one seeks to generate a realistic human speech signal. Feed-forward models are limited to the past $k$ samples, whereas recurrent models can use the entire history. Upon publication, the feed-forward, autoregressive WaveNet was a substantial improvement over LSTM-RNN parametric models.
-
Everthing Else. Recently Bai et al. proposed a generic feed-forward model leveraging dilated convolutions and showed it outperforms recurrent baselines on tasks ranging from synthetic copying tasks to music generation.
How Can Feed-Forward Models Outperform Recurrent Ones?
In the examples above, feed-forward networks achieve results on par with or better than recurrent networks. This is perplexing since recurrent models seem to be more powerful a priori. One explanation for this phenomenon is given by Dauphin et al.:
The unlimited context offered by recurrent models is not strictly necessary for language modeling.
In other words, it’s possible you don’t need a large amount of context to do well on the prediction task on average. Recent theoretical work offers some evidence in favor of this view.
Another explanation is given by Bai et al.:
The “infinite memory” advantage of RNNs is largely absent in practice.
As Bai et al. report, even in experiments explicitly requiring long-term context, RNN variants were unable to learn long sequences. On the Billion Word Benchmark, an intriguing Google Technical Report suggests an LSTM $n$-gram model with $n=13$ words of memory is as good as an LSTM with arbitrary context.
This evidence leads us to conjecture: Recurrent models trained in practice are effectively feed-forward. This could happen either because truncated backpropagation through time cannot learn patterns significantly longer than $k$ steps, or, more provocatively, because models trainable by gradient descent cannot have long-term memory.
In our recent paper, we study the gap between recurrent and feed-forward models trained using gradient descent. We show if the recurrent model is stable (meaning the gradients can not explode), then the model can be well-approximated by a feed-forward network for the purposes of both inference and training. In other words, we show feed-forward and stable recurrent models trained by gradient descent are equivalent in the sense of making identical predictions at test-time.
Stability is a natural criterion for learnability of recurrent models. Outside of the stable regime, gradient descent cannot be expected to work. Indeed, even for very simple unstable models, gradient descent fails to converge to a stationary point. While models trained in practice are not necessarily stable, the performance of unstable models is likely in spite of, not due to, their instability.
Using the Wikitext-2 language modeling benchmark, we show stability can be imposed on benchmark models without a loss in performance. Concretely, we conducted a hyperparameter search to find the best-performing unstable RNN and LSTM. Then, we re-trained both models while enforcing the stability conditions derived in our paper. In both cases, the unstable and stable models have the same test performance!
| Recurrent Model | Unstable (perplexity) | Stable (perplexity) |
|---|---|---|
| Tanh-RNN | 146.7 | 143.5 |
| LSTM | 92.3 | 95.1 |
Conclusion
Despite some initial attempts, there is still much to do to understand why feed-forward models are competitive with recurrent ones and shed light onto the trade-offs between sequence models. How much memory is really needed to perform well on common sequence benchmarks? What are the expressivity trade-offs between truncated RNNs (which can be considered feed-forward) and the widely-used convolutional models?
Answering these questions is a step towards building a theory that can both explain the strengths and limitations of our current methods and give guidance about how to choose between different classes of models in concrete settings.
-
The Transformer isn’t strictly a feed-forward model in the style described above (since it doesn’t make the $k$ step conditional independence assumption), but is not really a recurrent model because it doesn’t maintain a hidden state.
This article was initially published on the BAIR blog, and appears here with the authors’ permission.
tags: herotagrc